A new parameter estimation method to find all “good-enough” parameter sets
Advancement in measurement technologies and improvements in computational capability have led to complex models to simulate highly non-linear and non-stationary systems. In such a complex simulation system, calibration is an inseparable component. A common challenge in most calibration processes is the mismatch between model complexity and information delivered to the model from observations, referred to as equifinality (Beven, 1993). This means that when the complexity of the model is greater than the information within the observations, the calibration problem will be ill-posed and a single effective parameter vector cannot be found. This problem can be tackled from two points of view: to reduce the model complexity, or to accept the observation information insufficiency and retain all plausible parameter sets. In the latter one, we investigate the parameter space to find all behavioural parameter sets, rather than searching for a single optimum parameter set.
GLUE (Beven and Binley, 1992) and DREAM (Vrugt et al., 2008) are two examples of the method that used the latter approach. The outputs of these methods are samples from posterior parameter distribution. Unfortunately, in high dimensional and complex problems, these samples cannot provide an interpretation of the posterior distribution shape. Having such an interpretation assists modellers in understanding the global sensitivity of the model performance to its parameters and provides a broad understanding of the range of parameter vectors that produce acceptable model performance, which is very valuable in hydrological modelling.
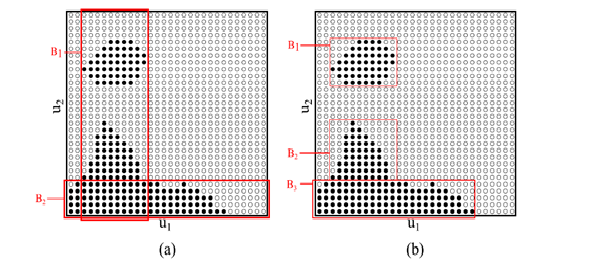
To address this limitation, we (Ashkan Shokri, Prof. Jeffrey P. Walker, Prof. Albert I. J. M. van Dijk, Ashley J. Wright, and A.Prof. Valentijn R. N. Pauwels) developed the Patient Rule Induction Method for Parameter Estimation (PRIM-PE). This method consists of an initial sampling procedure to generate a parameter sample that sufficiently represents the response surface with a uniform distribution within the “good-enough” region (i.e. performance better than a predefined threshold), and a rule induction component (PRIM) which is then used to define regions in the parameter space in which the “good-enough” parameter vectors are located. Figure 1 shows a schematic sample of good-enough regions.
Our paper, published in the Journal of Hydrological Processes, presents a new methodology to define where the behavioural parameter vectors are located in the parameter space.
Figure 1- Example of a sequence of boxes with different criteria: (a) low density and high interpretability and (b) high density and low interpretability
We show that the good-enough region can be considered as a confidence boundary of the optimal parameter vector. The total size of the resulting sequence of boxes from the PRIM-based method can be used as a measure of equifinality. As all parameter vectors located in the sequence of boxes share a minimum performance, they can be useful for various problems. Having every possible parameter vector for a number of nearby catchments allows using a parameter from the intersection of the other catchment’s good-enough region as a better choice for the ungauged catchment. Moreover, overlapping could be beneficial when for a specific location two series of observations are available. This may occur when a river has two gauging stations. For the upper, nested catchment, two sequences of boxes can be obtained. By overlapping the sequences of boxes for the doubly-gauged area, a smaller (less uncertain) good-enough region can be found. Furthermore, these boxes can be used as a source of parameter perturbation in Ensemble modelling. The good-enough regions could also be used as a prior estimate of the search region for other Markov chain Monte Carlo methods.
Article: ”Application of the patient rule induction method to detect hydrologic model behavioural parameters and quantify uncertainty”, Shokri A, Walker JP, van Dijk AIJM, Wright AJ, Pauwels VRN. Hydrological Processes. 2018;1–21. DOI: doi.org/10.1002/hyp.11464
